
Sopravvivenza e mortalità: come interpretare correttamente i dati degli studi
Data : 17 dicembre 2007
Autore : admin
Pagina: 1 - pag 1
I concetti di mortalità e sopravvivenza possono essere espressi in vari modi ed è importante conoscere il significato delle varie espressioni.
A) Analisi dei dati crudi
In questo caso si studia brutalmente il fenomeno senza valutare se durante il follow-up la sua intensità abbia subito variazioni.
Supponiamo di condurre uno studio sullo screening del cancro polmonare diagnosticando nei 100 soggetti del gruppo intervento 30 tumori e nei 100 del gruppo di controllo altri 20 tumori .
Supponiamo di registrare alla fine dello studio 15 decessi per cancro polmonare in entrambi i bracci.
Ovviamente questi dati 'crudi' rivelano una mortalità identica (15/100 nel braccio di intervento vs 15/100 nel braccio di controllo).
Questo modo di esprimere la mortalità è definito dal Rischio Assoluto di Morte (n.morti registrati nel periodo) / (totale pazienti a rischio nel periodo).
Un modo alternativo (su cui non ci soffermeremo ulteriormente) di esprimere la mortalità attraverso i dati crudi è rappresentato dall' Odds di Morte (=numero morti registrati nel periodo)/(numero non morti registrati nel periodo).
La sopravvivenza è sempre il complementare della mortalità e viene espressa pertanto da un Rischio Assoluto di Non Morte (n. non morti registrati nel periodo) / (totale pazienti a rischio nel periodo) o rispettivamente da un Odds di Non Morte (=numero non morti registrati nel periodo)/(numero morti registrati nel periodo).
Supponiamo ora di condurre sempre nello stesso campione di 200 soggetti un diverso tipo di analisi. Ossia anzichè considerare al denominatore nel calcolo della mortalità (Rischio assoluto di morte) tutti i pazienti inizialmente randomizzati al braccio consideriamo solo i pazienti a cui è stato diagnosticato il cancro.
Si tratta come detto di 30 casi nel gruppo screening e 20 casi nel gruppo controllo.
Espressa così la mortalità risulta minore nel braccio di intervento (15/30 = 50% versus 15/20=75%).
Possiamo anche dire (è la stessa cosa) che la sopravvivenza è risultata maggiore nel braccio di intervento ( 15 su 30 = 50% versus 15 su 20 = 25% nel braccio di controllo).
Quindi se invece di improntare l' analisi sul totale dei pazienti arruolati in ogni braccio, ci si riferisce al solo sottogruppo dei pazienti a cui è stato diagnosticato un cancro , apparentemente lo screening sembra essere in grado di aumentare la sopravvivenza nei malati dal 25% al 50% (oppure, il che è lo stesso, sembra in grado di ridurre la mortalita, nei malati dal 75% al 50%).
Pagina: 2 - pag 2
La sovradiagnosi
La spiegazione in questo esempio a tavolino è legata al fenomeno della Sovradiagnosi, una fonte di bias tipica degli studi di screening .
Vale a dire che nel gruppo screenato sono stati diagnosticati 10 tumori in più solo perché siamo andati a cercarli ma è probabile che (in quanto forme indolenti ossia meno aggressive di tumore) , senza screening non sarebbero mai diventate clinicamente evidenti.
Pertanto anche se i decessi per cancro nei due bracci alla fine del follow-up sono identici (rispettivamente 15 nel braccio di intervento e 15 nel braccio di controllo), nel sottogruppo dei pazienti riconosciuti affetti da cancro la minor mortalità riscontrata nel braccio di intervento è spiegata semplicemente dal maggior numero di casi posti al denominatore (15 su 30 vs 15 su 20) legato al maggior numero di diagnosi di cancro indotte dallo screening e dalla sostanziale minor aggressività presentata da alcuni di questi casi.
Per questo motivo l'end-point di uno studio di screening (vale a dire la mortalità o il suo speculare, la sopravvivenza) deve essere sempre riferito alla population study inizialmente considerata (i pazienti globalmente esposti o non esposti allo screening) e non ai pazienti a cui è stata diagnosticata la patologia oggetto di screening (case patient survival analysis).
Questo concetto è stato brillantemente sottolineato dagli autori del Mayo Lung Project [Natl Cancer Inst 2000;92:1308–16] , che concludono, a proposito dei programmi di screening rivolti al cancro al polmone, 'Case patient survival is not a reliable measure of efficacy'.
Nello studio della Mayo Clinic la sopravvivenza è stata espressa in termini di tempo (mediana di sopravvivenza) ma gli autori forniscono anche i dati crudi, che utilizzeremo come esempio reale di quanto sopra illustrato (tabella 1) . 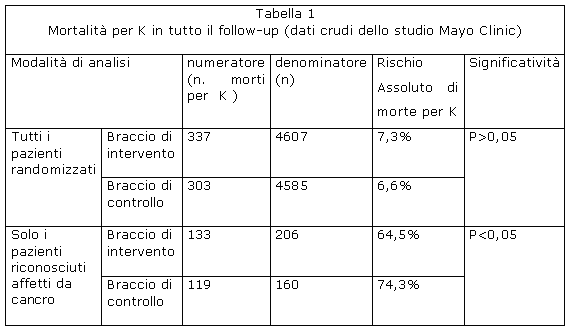
In questo studio randomizzato sullo screening del cancro polmonare l' intervento di screening era rappresentato da una radiografia del torace e da un esame dell'escreato. Venivano nella fattispecie messe a confronto due modalità operative diverse: nel braccio di intervento lo screening veniva effettuato ogni quattro mesi e nel braccio di controllo solo una volta all' anno. Alla fine dello studio si vide che i pazienti a cui era stato diagnosticato un cancro polmonare nel gruppo “screening ogni quattro mesi” avevano una sopravvivenza mediana di 16 anni mentre quelli con cancro polmonare del gruppo “screening ogni anno” avevano una sopravvivenza mediana di 5 anni. Tuttavia la mortalità per cancro polmonare alla fine dello studio era uguale nei due bracci. Come si spiega questo apparente paradosso? Si spiega anche qui col fatto che la mortalità era stata calcolata sul totale dei soggetti arruolati per ogni braccio mentre la sopravvivenza, espressa in termini di tempo, era stata calcolata solo sui soggetti riconosciuti affetti da cancro al polmone . Come correttamente rilevato dagli autori questa discrepanza può essere correlata alla distorsione legata alla sovradiagnosi.
Pagina: 3 - pag 3
Considerare tutti, non solo i malati
Quando si legge di aumento della sopravvivenza o di riduzione della mortalità, soprattutto in uno studio di screening, bisogna stare molto attenti a cosa queste misure si riferiscono e come sono state calcolate.
Un messaggio forte per una corretta interpretazione dei risultati di uno studio di screening è che l' outcome deve essere rilevato su tutti i pazienti randomizzati e non solo sui pazienti riconosciuti affetti dalla malattia.
Purtroppo bisogna stare bene attenti quando si legge uno studio di screening per capire in quale modo sono state determinate mortalità e sopravvivenza. Per esempio gli autori dello studio ELCAP [N Engl J Med 2006;355:1763-71.] hanno seguito 31.567 pazienti screenati per cancro del polmone con TAC spirale eseguita una volta all' anno. Lo screening portò alla diagnosi di 484 cancri del polmone, di cui 412 con tumore in stadio I. Per questi soggetti gli autori stimarono una sopravvivenza a 10 anni pari a 88%. Tra i 302 partecipanti con tumore allo stadio I sottoposti ad intervento chirurgico fu riscontrata una sopravvivenza a 10 anni pari al 92%. Gli autori conclusero che l' esecuzione annuale di TAC spirale permette una diagnosi precoce e un aumento della sopravvivenza.
Sono affidabili queste conclusioni? Molto poco sia perché questo studio mancava un gruppo di controllo, sia perché la sopravvivenza è stata calcolata sui malati, esponendosi pertanto al bias della sovradiagnosi.
Pagina: 4 - pag 4
Anticipazione diagnostica
Negli studi di screening che valutano la sopravvivenza sulla popolazione malata potrebbe entrare in gioco un altro bias, quello della anticipazione diagnostica (lead time bias).
Per capire di cosa si tratti prendiamo due gruppi di 10 pazienti sottoposti a screening oppure no per cancro del polmone attraverso una nuova tecnica.
Immaginiamo che il follow-up dello studio sia di 15 anni.
Supponiamo poi che in ognuno dei due gruppi all’inizio dello studio ci sia un paziente di 45 anni che abbia un cancro polmonare iniziato da 5 anni, quindi all'età di 40 anni, e che questo tumore non sia evidenziabile attraverso le usuali tecniche di indagine.
In definitiva quindi avremmo per ciascun gruppo 10 pazienti di cui 9 sani ed uno con cancro polmonare “ clinicamente invisibile” iniziato da 5 anni.
Immaginiamo quindi che attraverso lo screening (che permette diagnosi anticipate di tumore), nel paziente appartenente al gruppo screenato la neoplasia venga scoperta dopo un anno dall'inizio dello studio, quando il soggetto quindi abbia 46 anni.
Supponiamo poi che i paziente venga trattato ma muoia a 52 anni, quindi 6 anni dopo la diagnosi.
Supponiamo inoltre che nel secondo paziente malato di cancro ma non sottoposto a screening il tumore venga scoperto più tardivamente a 50 anni, vale a dire dopo 5 anni dall' inizio dello studio. Supponiamo che anche in questo caso il paziente muoia a 52 anni, vale a dire due anni dopo la diagnosi.
Se si misura la sopravvivenza dopo la diagnosi nel primo caso risulterà pari a 6 anni e nel secondo risulterà pari a 2.
Si potrebbe allora concludere che lo screening comporti un aumento netto di la sopravvivenza pari a 4 anni?
Ovviamente no: in realtà la mortalità per cancro polmonare, alla fine del periodo di follow-up considerato dallo studio , sarà comunque uguale nei due gruppi e corrisponderà al 10% della casistica (muore di cancro del polmone 1 paziente sui 10 allocati ad ogni gruppo).
Quindi lo screening ha scoperto prima il tumore, ma questo non si è tradotto in una riduzione della mortalità totale.
La figura 1 riassume questi concetti.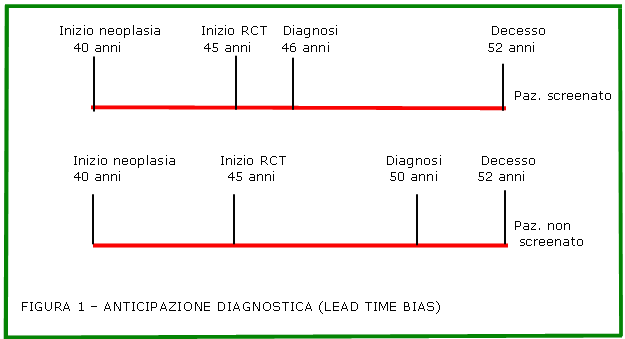
Pagina: 5 - pag 5
La mortalità va calcolata sul totale dei soggetti arruolati
Si potrebbe però obiettare che l’aumento della sopravvivenza così trovato dipende dall’averla misurata a partire dalla diagnosi. Se invece si fosse determinata la sopravvivenza a partire dal momento in cui i due soggetti sono stati arruolati nello studio la sopravvivenza sarebbe stata in ogni caso di 7 anni per entrambi. Purtroppo neppure usando questa modalità siamo sicuri di ottenere un dato affidabile.
Si ipotizzi quest’ altro esempio (tabella 2) , in cui, nei due pazienti, il tumore inizia sempre a 40 anni, la diagnosi avviene a 46 anni nel paziente screenato e a 50 in quello non screenato e il decesso, per entrambi, avviene a 52 anni. I dati sono gli stessi dell’esempio precedente, ma in questo secondo caso i due soggetti sono nati in anni diversi e quindi entrano nello studio con un’età diversa.
Il soggetto screenato è nato nel 1940, sviluppa il tumore nel 1980, viene arruolato nello studio nel 1985, la diagnosi di cancro polmonare viene fatta nel 1986 e muore nel 1992. Invece il soggetto non screenato è nato nel 1937, sviluppa il tumore polmonare nel 1977, entra nello studio nel 1985, il tumore viene diagnosticato nel 1987 e il paziente muore nel 1989.
Se si determina la sopravvivenza a partire dal 1985, data di inizio dello studio, nel paziente screenato si troverà che è di 7 anni mentre in quello non screenato è di 4 anni.
Eppure sappiamo che in realtà entrambi, dall’inizio del tumore, hanno avuto una sopravvivenza di 12 anni.
La tabella sottostante riassume questo secondo esempio.
Poiché, ovviamente, non possiamo sapere in quale momento il tumore ha cominciato a svilupparsi, è giocoforza affidarsi ad un end-point che non abbia queste potenziali distorsioni, vale a dire la mortalità calcolata rispetto al totale dei soggetti arruolati nella sperimentazione controllata.
Pagina: 6 - pag 6
Analisi del follow-up
Esprimere mortalità e sopravvivenza attraverso i dati crudi non fornisce alcuna informazione di come si siano distribuiti gli eventi durante il follow-up.
Per esempio in uno studio di prognosi che riguardi pazienti critici che hanno subito un intervento chirurgico la mortalità è sicuramente più alta nell' immediato postoperatorio, ma con l' analisi dei dati crudi questo fenomeno non viene rilevato.
Pensiamo come esempio più dettagliato ad uno studio controllato in cui siano stati arruolati 100 pazienti per braccio e che, dopo 3 anni, registri 15 decessi per braccio. Ovviamente si può concludere che la mortalità è del 15% in entrambi i casi e che l'intervento studiato (sia esso un farmaco oppure un intervento di screening o altro) non ha portato beneficio rispetto al controllo. Però supponiamo che nel braccio intervento si siano registrati 2 decessi in tutto nel primo anno, altri 5 decessi nel secondo anno, 8 decessi nel terzo.
Invece nel braccio controllo si siano registrati: 6 decessi nel primo anno, 6 decessi nel secondo anno e 3 decessi nel terzo anno. Pur essendo vero che il numero di decessi totali alla fine del terzo anno è identico nei due gruppi il rischio di morte è diverso nei tre diversi periodi: è minore per il primo gruppo nel primo e secondo anno mentre nel terzo anno risulta avvantaggiato il secondo gruppo. Affidarsi, allora, solo alla mortalità alla fine dello studio fa correre il rischio di non tener conto dei benefici dell'intervento nei primi due anni. Probabilmente ognuno di noi preferirebbe affidarsi all'intervento perché, almeno per i primi due anni, avrebbe una mortalità minore rispetto al controllo, anche se poi, alla fine del terzo anno, il vantaggio scompare.
Per ovviare a queste difficoltà vengono costruite delle curve di sopravvivenza (dette curve di Kaplan-Meier).
Si costruisce un sistema cartesiano in cui l'asse delle ordinate rappresenta la sopravvivenza (parte ovviamente dal valore 100% all' inizio dello studio) e l'asse delle ascisse il tempo. La costruzione della curva dipende dal timing nel quale si verificano gli eventi. In altre parole non si stabilisce un intervallo fisso a priori (per esempio contare gli eventi ogni 2 settimane oppure ogni 2 mesi, ecc.) ma è la comparsa di ciascun evento che determina la durata degli intervalli (per esempio potrebbe essere che il primo decesso compaia dopo 5 giorni dall'inizio dello studio e allora l'intervallo avrà durata 5 giorni, il secondo dopo 7 giorni dall'inizio e allora questo intervallo durerà 2 giorni, e così via). In questa maniera viene costruita una curva che ha un andamento a scalini. Un esempio è la figura 2 in cui vengono rappresentate due curve di sopravvivenza, una verde ed una rossa. Anche se alla fine dello studio la sopravvivenza è la stessa per entrambe le curve si nota chiaramente che ai tempi intermedi essa è superiore per la curva verde rispetto alla curva rossa. Se la prima rappresenta la curva ottenibile con uno screening e la seconda quella nel gruppo senza screening, anche se al termine dello studio non c'è differenza, è evidente che nei tempi intermedi lo screening otterrebbe dei benefici, purché il tempo guadagnato sia ovviamente degno di essere vissuto e la qualità di vita decente.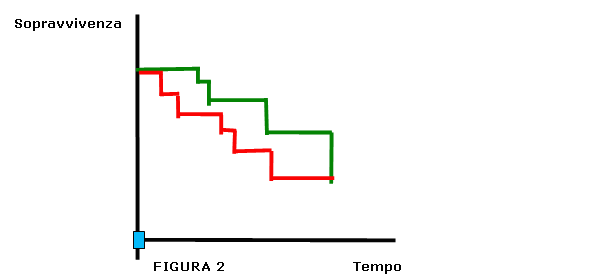
Pagina: 7 - pag 7
Mortalità istantanea
Nella stessa maniera si possono costruire curve di Kaplan per ogni altro outcome: infarti, stroke, interventi di rivascolarizzazione coronarica, fratture di femore e così via.
Nel caso della rappresentazione della sopravvivenza ogni punto della curva di Kaplan corrisponde alla registrazione di un evento (nella fattispecie: di un decesso).
La Mortalità Istantanea al tempo t esprime la probabilità di morire in quel punto della curva ed è calcolabile dal rapporto (numero di morti registrati in quel tempuscolo) / (totale pazienti a rischio all'inizio di quel tempuscolo). NB: è lo stesso concetto espresso da Rischio Assoluto, che come la Mortalità Istantanea è una proporzione: ma mentre il Rischio Assoluto misura la mortalità registrata durante tutto il follow-up, la Mortalità Istantanea esprime la mortalità registrata nel tempuscolo t.
Il calcolo della Sopravvivenza Cumulativa al tempo t presuppone ulteriori passaggi.
Viene calcolata innanzitutto la Sopravvivenza Istantanea al tempo t , che è complementare alla Mortalità Istantanea.
Se esprimiamo la Mortalità istantanea con i decimali (esempio: 0.01 anziché 1%), la Sopravvivenza Istantanea è espressa dalla differenza (1-Mortalità Istantanea), ossia dal complementare a uno della Mortalità Istantanea (nell' esempio: 1-0.01 = 0.99= 99%) .
Ciò è ovvio, in quanto mortalità e sopravvivenza sono due fenomeni speculari.
La Sopravvivenza Cumulativa al tempo t (ripetiamo, quello che viene raffigurato graficamente nella curva di Kaplan) è allora espressa dal prodotto di tutte le sopravvivenze istantanee misurate fino a quel momento (ossia della sopravvivenza istantanea misurata al tempo t e di tutte le sopravvivenze istantanee misurate in tutti i punti precedenti della curva).
Per esempio si supponga di voler determinare la sopravvivenza fino a 90 giorni di un gruppo di 100 pazienti che hanno subito un ictus: il primo decesso avvenga il giorno 9, il secondo il giorno 12, il terzo il giorno 18, il quarto il giorno 26, il quinto il giorno 44, il sesto il giorno 57, il settimo il giorno 68, l'ottavo il giorno 72, mentre dal giorno 73 al 90 non avviene alcun decesso.
Facciamo un pò di conti.
Al giorno 9 avviene il primo decesso: la mortalità istantanea è allora 1/100 (=morti/ esposti al rischio) , mentre la sopravvivenza istantanea è 99/100 (= sopravvissuti/ esposti al rischio). Restano per la successiva analisi 99 esposti al rischio.
Al giorno 12 avviene il secondo decesso: la mortalità istantanea è allora 1/99 (=morti/ esposti al rischio), mentre la soravvivenza istantanea è 98/99 (= sopravvissuti/ esposti al rischio). Restano per la successiva analisi 98 esposti al rischio.
Al giorno 18 avviene il terzo decesso: la mortalità istantanea è allora 1/98 (=morti/ esposti al rischio), mentre la soravvivenza istantanea è 97/98 (= sopravvissuti/ esposti al rischio). Restano per la successiva analisi 97 esposti al rischio.
Proviamo ora a calcolare la sopravvivenza cumulativa al giorno 18: corrisponderà a: 99/100*98/99*97/98 = 0,97 ossia 97% (tabella 3).
E cosi' via.
Pagina: 8 - pag 8
I calcoli sono riassunti nella tabella 3, dove compare una voce non ancora descritta, quella dei pazienti 'censorizzati'. 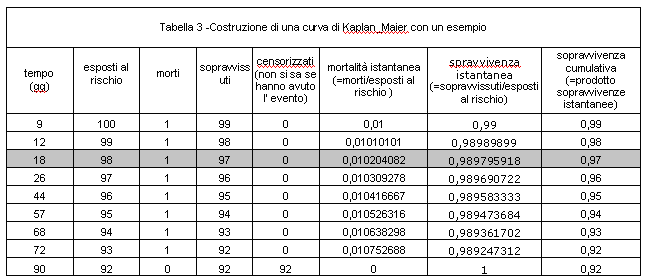
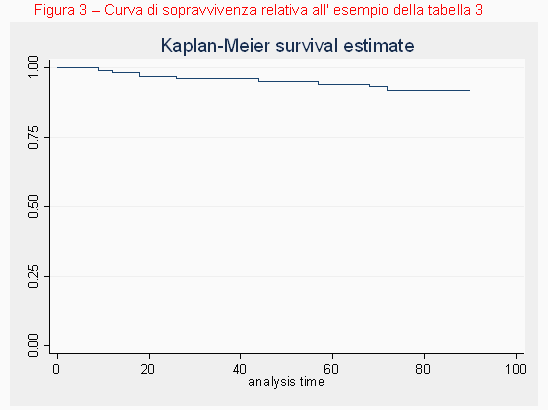
Nell'analisi delle curve di sopravvivenza i pazienti 'censorizzati' sono quelli che durante il periodo di osservazione non hanno avuto l' evento. Nel semplice esempio che abbiamo riportato i pazienti censorizzati sono 92 in quanto al 90° giorno di osservazione abbiamo contato 8 decessi su 100 pazienti per cui i pazienti che non hanno subito l' evento durante questo periodo sono 100-8 =92. Durante un periodo di follow-up in condizioni reali di ricerca capita spessissimo che alcuni pazienti escano dall' osservazione anche durante il follow-up stesso (per esempio in quanto vengono persi oppure , altro esempio, perchè hanno subito un evento diverso da quello studiato ma tale da impedire la prosecuzione del periodo di osservazione). Questi pazienti 'censorizzati' durante il follow-up contribuiscono comunque al calcolo della sopravvivenza cumulativa in quanto di loro occorre tener conto nel computo della sopravivvenza istantanea successiva al tempo di censorizzazione. Per semplicità nell' esempio non abbiamo considerato queste circostanze in quanto un' eccessiva analisi dell' argomento esula dallo scopo dell'articolo.
La CURVA DI SOPRAVVIVENZA può essere anche costruita invertendo l' outcome, ossia creando una CURVA DI MORTALITÀ. L'andamento è allora speculare e anche in questo caso la pendenza, nell' esempio considerato, sarà maggiore nell' immediato postoperatorio
Se vogliamo invertire l' outcome per raffigurare graficamente una CURVA DI MORTALITÀ la Mortalità Cumulativa per ogni punto t sarà data da (1- Sopravvivenza Cumulativa al tempo t).
In questo caso ogni singola curva curva avrebbe l'aspetto illustrato nella figura 4.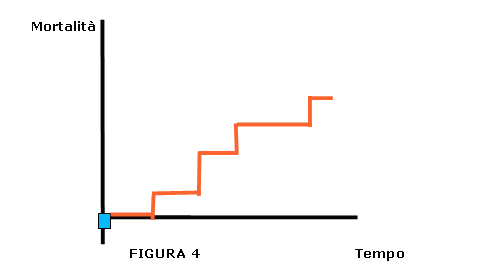
Pagina: 9 - pag 9
Il confronto tra curve
Per confrontare due curve che rappresentano la sopravvivenza di due gruppi di soggetti influenzati dalla presenza o meno di una determinata variabile (es: sottoposti a screening versus non sottoposti a screening) esiste innanzitutto un semplice test statistico (il Log Rank test).
Questo test , come qualsiasi altro test di significatività, produce un valore di P che esprime la probabilità con cui le differenze tra le due curve possano essere spiegate dal caso. Se P<0.05 , come al solito, il risultato si definisce 'significativo' in quanto la probabilità che sia legato al caso è molto bassa e quindi trascurabile (0.05 = 1/20).
Però il log-rank test, nel confronto fra due curve, permette solo di rifiutare o confermare l’ipotesi nulla, cioè dice solo se la differenza è o meno significativa, ma non fornisce informazioni circa l’entità di tale differenza e nemmeno l' intervallo di confidenza intorno a questa stima .
Inoltre il confronto di due curve con il Log rank test permette soltanto analisi univariate, ossia non tiene conto della potenziale influenza esercitata da altri fattori in grado di influenzare la sopravvivenza in modo indipendente dalla variabile che caratterizza i soggetti esaminati attraverso il confronto. Se per esempio l'età dei soggetti la cui sopravvivenza è espressa da una delle due curve è molto maggiore dell'età dei soggetti che contribuiscono al calcolo della sopravvivenza nella seconda curva , la diversa sopravvivenza rilevata può essere spiegata non solo dall' avere o meno eseguito lo screening ma, semplicemente, da queste differenze di età.
Per confrontare due curve per una variabile a parità di tutte le altre variabili potenzialmente in grado di influenzare la sopravvivenza si usa una tecnica sofisticata di analisi applicata alla sopravvivenza che si chiama modello di COX.
Nel modello di COX per ciascuna curva viene determinato l'Hazard Rate che esprime la pendenza della curva e concettualmente rappresenta per ogni tempo t il Tasso* Istantaneo dell' Evento (nel nostro esempio corrisponde al tasso Istantaneo di Morte).
Ora: il modello di Cox presuppone che in ciascun punto della curva il rapporto tra i due Tassi istantanei dell' evento (ossia tra i due Hazard Rate) sia costante, vale a dire che i due Hazard Rate, quando variano, varino nella stessa misura.
E' per questo che il COX viene definito 'modello a rischi proporzionali'
Allora, il confronto tra le due curve può essere espresso per ogni punto dal loro rapporto (Hazard Ratio), che sarà costante per ogni punto della curva.
L' Hazard Ratio (HR), che dunque è il rapporto tra due Hazard rate, è di solito impropriamente assimilato ad un Rischio Relativo ; il concetto che esprime è in effetti simile ma mentre il Rischio relativo è il rapporto tra i due Rischi Assoluti dell' evento in due gruppi di soggetti a confronto l' Hazard ratio è il rapporto tra le pendenze di due curve di sopravvivenza espresse dai rispettivi hazard rate. Anche per l’HR può essere calcolato un intervallo di confidenza, che viene prodotto dal modello di Cox.
* Nota: Cos'è un tasso? Il Tasso Istantaneo di Morte non coincide con la Mortalità Istantanea (che è una proporzione e corrisponde al Rischio Assoluto di morte al tempuscolo t).
Un tasso non è una proporzione: i suoi valori possono infatti andare da 0 a infinito, mentre in una proporzione i valori possono andare da zero a 1 (o, se si preferisce, da 0% a 100%). Infatti al denominatore di un Tasso non è espresso il numero di soggetti a rischio per l' outcome, ma piuttosto la somma dei periodi di follow-up che caratterizzano ciascun soggetto.
Per esempio se abbiamo cinque soggetti seguiti rispettivamente per uno, tre, due, quattro, due anni la somma di tutti i periodi individuali di follow-up è 12 anni.
Se due di questi soggetti alla fine del periodo di osservazione muoiono possiamo esprimere la mortalità sia come Rischio Assoluto che come Tasso ma la differenza è enorme. Infatti la mortalità espressa come Rischio Assoluto è 2/5uomini = 40%, mentre la mortalità espressa come Tasso è 2/12anni uomo = 16 su cento anni uomo.
Pagina: 10 - pag 10
I vantaggi del modello di COX
I vantaggi associati all' utilizzo del modello di Cox al posto del confronto tra due curve di sopravvivenza effettuato attaverso il log-rank test sono enormi.
In primo luogo il calcolo dell' HR permette di stabilire non solo se la pendenza tra le due curve è significativamente diversa ma permette anche di stimare l’entità di questa differenza e l’ampiezza dell’intervallo di confidenza intorno a questa stima, che esprime la precisione dei risultato del confronto.
In secondo luogo (e soprattutto) questo sofisticato modello permette di valutare il contributo alla sopravvivenza fornito da una variabile a parità dell' influenza esercitata da tutte le altre inserite nell' analisi.
Per esempio attraverso il modello di Cox si può stabilire se la sopravvivenza * dei pazienti che hanno subito un infarto sia modificata o meno dall' assunzione di una statina . In questo caso il modello crea e confronta due curve di sopravvivenza che rappresentano i pazienti che assumono statine e rispettivamente quelli che non assumono statine . Il confronto tra le due curve espresso dall' Hazard Ratio è eseguito tenendo contemporaneamente conto dell' influenza esercitata sulla sopravvivenza (=variabile dipendente) da altre variabili inserite nell' analisi perchè ritenute parimenti in grado di influenzare la sopravvivenza (=covariate o variabili indipendenti) . Per esempio se abbiamo inserito nel modello le covariate 'età' ; 'assunzione o meno di statine'; 'presenza o meno di scompenso cardiaco' ; 'presenza o meno di diabete' il modello di Cox valuta in che misura l' assunzione di statine ha influenzato la sopravvivenza dei soggetti infartuati a parità dell' influenza esercitata da tutte le altre condizioni potenzialmente importanti (età, presenza o assenza di scompenso cardiaco, presenza o assenza di diabete, eccetera ) . Ovviamente possiamo analizzare allo stesso modo l' influenza esercitata sulla sopravvivenza dei soggetti infartuati da qualsiasi altra covariata inserita nel modello (è, per esempio, possibile valutare il contributo del diabete sulla mortalità dei soggetti infartuati aggiustato per il contributo esercitato da tutte le altre variabili)
Per concludere riassumiamo i concetti che devono rimanere:
1) in uno studio di screeening la mortalità o la sopravvivenza dovrebbero essere determinate sul totale dei soggetti studiati e non solo sui pazienti riconosciuti affetti dalla patologia in quanto quest'ultima modalità espone a possibili bias di sovradiagnosi e di anticipazione diagnostica
2) nel valutare i risultati di uno studio in cui si registra un fenomeno lungo un arco temporale consistente è necessario giudicare gli end-point non solo sulla base dei dati “crudi” registrati alla fine del follow-up ma anche sul confronto fra curve di Kaplan-Meier.
Alessandro Battaggia, Luca Puccetti e Renato Rossi (in ordine alfabetico)
* Nota: (*) la funzione di sopravvivenza può essere calcolata dalla funzione di hazard calcolata dal modello di Cox