| |
|
|
 |
Valori predittivi di un test - Capitolo 2 |
|
|
Inserito il 02 febbraio 2008 da admin. - scienze_varie - segnala a:    
Valori predittivi positivi e negativi di un test non dipendono solo dalla sensibilità e dalla specificità ma soprattutto dalla prevalenza della malattia nella popolazione a cui il test viene applicato.
In una pillola precedente [1] sono stati introdotti alcuni concetti relativi ai test diagnostici:
• la sensibilità (che si applica sui soggetti malati e determina la percentuale di essi che il test riesce a scoprire)
• la specificità (che si applica alla popolazione dei sani e determina la percentuale di essi che il test riesce a scoprire)
• il valore predittivo positivo o VPP (che definisce la probabilità che un test positivo sia un positivo vero)
• il valore predittivo negativo o VPN (che definisce la probabilità che un test negativo sia un negativo vero).
Al medico pratico i valori di sensibilità e di specificità interessano relativamente perchè la domanda che egli si pone, di fronte al risultato di un test, è sapere quante probabilità ci sono che se il test è positivo quella persona sia realmente malata e quante, se il test risulta negativo, che quella persona sia sana. In altre parole al medico interessa sapere, più che la sensibilità e la specificità del test, il VPP e il VPN. Tuttavia questi due parametri dipendono dalla prevalenza della malattia nella popolazione esaminata. Questo è un concetto di fondamentale importanza che si cercherà di chiarire con alcuni esempi.
Primo esempio
In una popolazione di 1000 individui ci sono 400 persone affette dalla malattia "X" e 600 che sono sane. E' disponibile un test che viene pubblicizzato come in grado di diagnosticare la malattia in esame. Se il test avesse una sensibilità ed una specificità del 100% non ci sarebbe alcun problema. Applicato ai 400 malati sarebbe in grado di identificarli tutti (cioè non vi sarebbero falsi negativi) e applicato ai 600 sani risulterebbe sempre negativo (vale a dire non vi sarebbero soggetti con test positivo ma in realtà senza la malattia).
Purtroppo un test ideale di questo tipo è molto difficile da trovare. Si supponga allora che il test abbia una sensibilità dell'80% e una specificità del 90%.
• Applicando la sensibilità ai 400 malati si avrà che l'80% (= 320) ha un test positivo (veri positivi) ed il rimanente 20% (= 80) un test negativo (falsi negativi).
• Applicando con la stessa procedura la specificità ai 600 senza la malattia, si avrà che il 90% (= 540) ha il test negativo (veri negativi) ed il rimanente 10% (= 60) ha il test positivo (falsi positivi).
In definitiva avranno il test positivo in 380 (di cui 320 veri positivi e 60 falsi positivi) e il test negativo in 620 (di cui 540 veri negativi e 80 falsi negativi).
Il VPP del test è l'84%.
Il VPN è dell'87%.
Tutto questo tradotto per il medico pratico vuol dire che se si applica il test ad una delle 1000 persone del campione iniziale e lo si trova positivo vi è una probabilità dell'84% che abbia la malattia mentre se lo si trova negativo la probabilità che il soggetto non abbia la malattia è dell'87%.
Secondo esempio
In una popolazione di 1000 individui ci sono 80 persone affette dalla malattia e 920 sane. Il test disponibile per la diagnosi della malattia ha uan sensibilità dell'80% e una specificità del 90%, come nell'esempio precedente. Si noti però che in questo caso la prevalenza della malattia è molto minore (8% vs 40%).
• Applicando la sensibilità agli 80 malati si avrà che l'80% (= 64) ha un test positivo (veri positivi) e il 20% (= 16) ha il test negativo (falsi negativi).
• Applicando la specificità ai 920 sani si avrà che il 90% (= 828) ha il test negativo (veri negativi) e il 10% (= 92) ha il test positivo (falsi positivi).
In definitiva avranno il test positivo in 156 (di cui 64 veri positivi e 92 falsi positivi) e il test negativo in 844 (di cui 828 veri negativi e 16 falsi negativi).
Il VPP è del 41% e il VPN del 98%.
Come si vede in tutti e due gli esempi la sensibilità e la specificità del test sono le stesse, ma varia la prevalenza della malattia nella popolazione esaminata. Nel primo esempio la malattia era presente nel 40% della popolazione e se il test risultava positivo vi era una probabilità dell'84% che il soggetto fosse malato mentre se risultava negativo vi era una probabilità dell'87% che il soggetto fosse realmente sano. Nel secondo esempio la malattia è presente solo nell'8% della popolazione quindi, pur a parità di sensibilità e di specificità del test, il VPP è molto più basso (41%) mentre il VPN è più elevato (98%).
Si pensi ora ad una malattia "XYZ" con una prevalenza dell'1% sull'intera popolazione e ad un test con sensibilità dell'80% e una specificità del 90%. Il VPP del test sarà di circa il 7% il che significa che se si chiede indiscriminatamente il test a tutta la popolazione c'è una probabilità del 7% che ad un risultato positivo corrisponda un malato. Se, invece di applicare il test per la malattia "XYZ" indiscriminatamente, lo si richiede solo quando esiste un motivato sospetto clinico si seleziona una popolazione in cui la prevalenza non sarà più dell'1%, ma molto più elevata. Pertanto anche il VPP sarà ben diverso. Si ipotizzi per esempio che in una popolazione che presenta la triade di sintomi A+ B + C la prevalenza della malattia "XYZ" sia del 70%. In questo caso il test, a parità di sensibilità e specificità, avrà un VPP pari a circa il 94%.
Da tutto questo se ne deve dedurre che i test diagnostici andrebbero richiesti solo a ragion veduta, quando vi è un fondato sospetto clinico da confermare. Infatti i valori predittivi di un test non dipendono solo dalla loro sensibilità e specificità, ma soprattutto dalla prevalenza della malattia nella popolazione in esame: un test con una sensibilità e una specificità molto buone (per esempio rispettivamente del 90% e del 95%) che serve per la diagnosi di una condizione che ha una prevalenza nella popolazione generale dell'1% avrebbe, se applicato indiscriminatamente a tutti, un VPP molto basso, di circa il 15%.
La tabella sottostante mostra alcuni valori predittivi positivi e negativi di un test al variare della sensibilità, della specificità e della prevalenza della malattia.
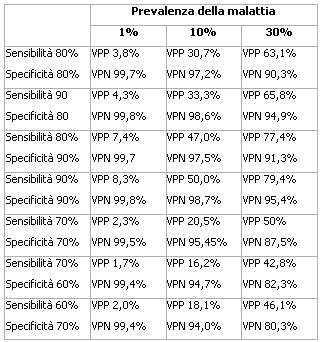
Come si può notare il valore predittivo positivo di un test è influenzato relativamente poco da sensibilità e specificità mentre risente molto di più dalla prevalenza della malattia nella popolazione testata: quando la prevalenza è bassa il VPP è molto basso pur in presenza di buoni valori i sensibilità e specificità.
Renato Rossi
Bibliografia
1. http://www.pillole.org/public/aspnuke/news.asp?id=3276
Commento di Luca Puccetti
Tutto quanto sopra esplicitato è matematicamente vero, ma nell'arte medica, che è appunto un' arte oltre che una scienza, prendono forza ed importanza elementi psicologici della relazione medico paziente che sono fondamentali anche se non matematicamente fondati. In medicina un test non serve solo a fare una diagnosi o ad escluderla , ma può far parte, a seconda dei casi del processo di cura stesso, come elemento di rassicurazione del paziente (e talora anche del medico). Inoltre dobbiamo sempre pensare, anche applicando meri ragionamenti matematici, che esistono pur sempre le malattie rare, ma non per questo è impossibile diagnosticarle od escluderle specie se si dispone di test dirimenti.
Commento di Marco Grassi
Quanto esposto diventa paradigmatico nel caso di un marker di neoplasia.
Si consideri per esempio il CA 125 per la diagnosi di cancro ovarico. Questo test ha una sensibilità del 50% e una specificità del 95%.
Se si dosa il CA125 in una donna che sia già stata operata di cancro ovarico, per calcolare il VPP e il VPN del test, bisogna considerare che in questa popolazione la prevalenza della malattia (in questo caso si tratterebbe di una recidiva) è stimata al 60%. Questo vuol dire che su 100 donne 60 sono malate.
Applicando la sensibilità alle 60 donne malate risulterà che 30 hanno il test positivo (veri positivi) e 30 il test negativo (falsi negativi) mentre applicando la specificità alle 40 donne sane risulterà che 38 sono negative al test (veri negativi) e 2 sono positivi al test (falsi positivi).
In tutto si vranno quindi 32 donne positive al test (di cui 30 vere positive) e il VPP sarà di 93,75. I casi negativi al test saranno 68 (di cui 38 veri negativi) e il VPN del test sarà del 55%.
Si supponga invece di dosare il CA 125 in una donna non operata da cancro ovarico e senza sintomi sospetti. In una popolazione generale sana la prevalenza di questo tipo di neoplasia è di 40 casi su 100.000.
Applicando la sensibilità del 50% ai 40 casi di malattia si avranno 20 casi con test positivo (veri positivi) e 20 con test negativo (falsi negativi).
Appliacando la specificità ai 99.960 casi sani si avrà che 94.962 sono negativi al test (veri negativi) e ben 4.998 sono postivi (falsi positivi).
In totale i positivi sono 5.018 (di cui 4.999 falsi positivi) e il VPP sarà di 0,39.
I casi negativi totali saranno 94.982 (di cui solo 20 sono falsi negativi) e il VPN sarà del 99,97%.
In conclusione il risultato di un marker di neoplasia è interpretabile solo considerando il contesto in cui è stato richiesto. Quando richiediamo un marker di neoplasia dobbiamo stimare la probabilità a priori che il/la paziente abbia un tumore. Se il/la paziente appartiene ad una popolazione in cui la probabilità di tumore è alta ( perchè, per esempio, ha sintomi e segni suggestivi) un risultato positivo è molto probabilmente corretto e un risultato negativo è probabilmente errato. Se il/la paziente appartiene ad una popolazione in cui la probabilità di tumore è molto bassa ( perchè, per esempio, asintomatico) un risultato positivo è molto probabilmente errato e un risultato negativo è probabilmente corretto. In questo caso, tuttavia, un risultato positivo, ancorchè improbabile, deve essere verificato con ulteriori accertamenti.
|
|
|
Letto : 8125 | Torna indietro |  |  | 
|
|
|
|
|
|
|
|
Home
Entra
Iscriviti
