| |
|
|
 |
Il rapporto di verosimiglianza |
 |
 |
Inserito il 28 marzo 2008 da admin. - scienze_varie - segnala a:    
 Un approfondimento sul significato e l'uso del rapporto di verosimiglianza o LR.
Un approfondimento sul significato e l'uso del rapporto di verosimiglianza o LR.
In una pillola precedente si è visto che un determinato test possiede una sua sensibilità e una sua specificità [1]. Conoscendo questi due dati e la prevalenza della malattia in una determinata popolazione che il test deve diagnosticare è possibile calcolare il numero dei veri positivi, dei falsi positivi, dei veri negativi e dei falsi negativi e da questi risalire al valore predittivo positivo e al valore predittivo negativo del test.
Abbiamo anche visto che la sensibilità e la specificità di un test possono essere messe tra loro in relazione in un grafico che costituisce la cosiddetta curva ROC [2].
Però esiste un altro modo di mettere in relazione sensibilità e specificità tra di loro: si tratta del likelihood ratio (o rapporto di verosimiglianza), abbreviato di solito con la sigla LR. Si possono avere due tipi di LR, uno positivo (LR+) e uno negativo (LR -).
Il LR + mette in relazione la probabilità di trovare il test positivo nei malati con la probabilità di trovarlo positivo nei sani.
Calcolarlo è facile: per esempio se un test ha una sensibilità del 90% e una specificità del 90% il LR + sarà dato dal rapporto: sensibilità/100 - specificità, cioè 90/100 -90 = 90/10 = 9.
Il significato è altresì intuitivo: su 10 sani il test è positivo solo 1 volta, su 10 malati il test è positivo ben 9 volte.
Conoscere il LH + di un test permette di arrivare a calcolare la probabilità post-test della malattia una volta che sia nota la probabilità pre-test.
Il modo di procedere è un po' indaginoso e ci si avvarrà di un esempio.
Supponiamo che in una determinata popolazione la prevalenza di una certa malattia sia del 10%. Ciò significa che la probabilità pre-test di trovare tale malattia nel campione esaminato è del 10% (in altre parole la probabilità pre-test non è altro che la prevalenza della malattia in quella popolazione). Supponiamo anche che il LH + di un determinato test per tale malattia sia 4.
Per prima cosa bisogna trovare il cosiddetto odds pre-test. Il concetto di "odds" è tipico del modo anglosassone e si richiama all'ambiente delle corse. Noi siamo abituati a dire che nella popolazione esaminata la probabilità di trovare un malato è del 10%. Invece l'odds è la probabilità di malattia rispetto alla non malattia. Nel caso in esame la non malattia riguarda 90 persone su 100. Quindi l'odds si calcola dividendo 10 per 90 (cioè per i non malati).
L'odds pre-test sarà quindi: 10/90 = 0,11.
Se si moltiplica l'odds pre-test per la LH + (che è 4) si trova l'odds post -test: 0,11 x 4 = 0,44. Conoscendo l'odds post-test è possibile calcolare la probabilità post-test con la seguente formula: odds post test/odds post test + 1.
Sarà quindi: 0,44/1 + 0,44 = 0,44/1,44 = 30%.
Possiamo quindi dire che se la probabilità pre-test della malattia è 10% e il LR + è 4 la probabilità post test è 30%. Si noti che la probabilità post-test non è altro che il valore predittivo positivo del test, che si può ottenere, come si è visto in una pillola precedente [1], anche per altra via conoscendo i veri positivi, i veri negativi, i falsi positivi e i falsi negativi.
E' ovvio che tanto maggiore è il LR + tanto più utile è il test: un valore appena superiore a 1 cambia di poco la probabilità pre-test, un valore compreso tra 5 e 10 provoca un aumento moderato della probabilità pre-test mentre la performance maggiore la ottiene un test con LR + superiore a 10 perché in questo caso si ottengono notevoli cambiamenti dal pre-test al post-test. Nel caso esemplificato la probabilità pre-test passa dal 10% al 30% del post-test.
Ovviamente il LR + può avere anche risultati più piccoli di 1: in questo caso la probabilità post-test diventa addirittura inferiore a quella pre-test.
Si pensi per esempio ad un test con sensibilità del 55% e specificità del 30%: il LR + sarà di 0,78. Se la probabilità pre-test è del 10%, dopo il test si riduce al 7,9%.
Conoscendo la probabilità pre-test e il LR è possibile calcolare la probabilità post-test senza dover fare i calcoli prima descritti utilizzando un apposito nomogramma messo a punto da Fagan.
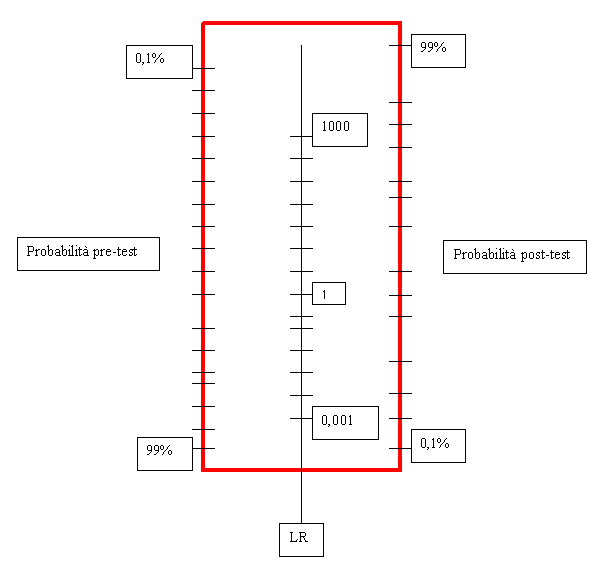
La figura mostra come funziona il nomogramma di Fagan: unendo con un righello la probabilità pre-test e il LR si ottiene la corrispondente probabilità post-test senza dover ricorrere ai calcoli.
Scarica il nomogramma di FAGAN in formato PDF a pagina intera: http://www.pillole.org/public/aspnuke/downloads.asp?id=291
Ovviamente come esiste un LR + esiste anche un LR - che mette in relazione la probabilità di trovare il test negativo nei malati con la probabilità di trovarlo negativo nei sani.
Si può calcolare con la formula: 100 - sensibilità/specificità.
Nel caso per esempio di sensibilità 90% e specificità 80% esso sarà dato dalla formula:
10/80 = 0,125.
Facciamo un esempio per capirci.
Si supponga una malattia con probabilità pre-test del 10% mentre il test ha una LR - di 0,05.
Odds pre-test = 10/90 = 0,11.
Odds post-test = 0,11 x 0,05 = 0,0055
Probabilità post test = 0,0055/1+0,0055 = 0,0054
In altre parole una probabilità pre-test del 10%, se il test è negativo, passa ad una probabilità post-test di malattia incredibilmente bassa, pari a poco più del 5 per mille.
Per concludere sul significato del Likelihood Ratio:
1) LR + si riferisce ai test positivi e tanto più è grande tanto più aumenta la probabilità pre-test
2) LR - si riferisce ai test negativi e tanto più è piccolo tanto più riduce la probabilità test.
Vediamo di spiegarci con degli esempi.
Eseguo un test che ha un LR positivo di 40 e un LR negativo di 0,003. Se trovo il test positivo so che aumenta di molto la probabilità pre-test. Se trovo il test negativo so che si riduce in maniera considerevole la probabilità pre-test.
Le cose cambiano per valori diversi di LR: facciamo l’ipotesi di un test con LR + di 1 e LR – di 1. Sia che trovi il test positivo sia che lo trovi negativo so che questo non cambierebbe la probabilità pre-test, quindi si tratterebbe di un test inadatto a guidare le mie decisioni diagnostiche.
Tutto questo discorso ovviamente non può prescindere dal valore della probabilità pre-test di malattia perché le cose possono essere diverse a seconda se questa è bassa o alta. Per esempio se applico un test con LR + di 40 ad una probabilità pre-test di 1% si ottiene una probabilità post-test del 28,5%: in ogni caso nel 71,5% dei casi un test positivo sarebbe comunque un falso positivo!
Ma perché si usa il LR invece di usare semplicemente la sensibilità e la specificità? La maggiore utilità si ha quando si è di fronte ad un test non dicotomico. In questi casi ogni valore ha una sua sensibilità e una sua specificità: ricorrendo al LR per ogni valore è possibile fare un paragone diretto. In pratica si può paragonare sensibilità e specificità del test per i vari valori senza dover ricorrere alla costruzione della curva ROC ma semplicemente confrontando i valori del LR.
Si prendano per esempio la sensibilità e la specificità del PSA per vari valori: si può costruire la curva ROC, come visto in una pillola precedente [2], oppure si può calcolare per ognuno di essi il LR , in modo da paragonarli:
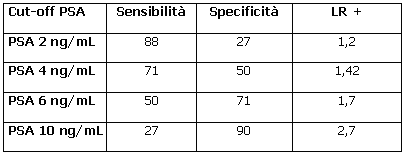
Come di può vedere il LR + più favorevole sarebbe quello del valore 10 ng/mL perché è quello che più aumenta la probabilità pre-test. Tuttavia in questo caso si avrebbe un elevato numero di falsi negativi: ben il 73% dei malati sfuggirebbe al test. Come si è visto nella pillola sulla curva ROC il miglior compromesso tra sensibilità e specificità in questo caso si realizza scegliendo un valore compreso tra 4 ng/mL e 6 ng/mL [2].
Un esempio famoso che viene riportato in tutti i testi di statistica medica è quello della ferritina per la diagnosi di anemia ferropriva: valori di ferritina inferiori a 15 hanno un LR + di 52 e quindi il test conferma la carenza di ferro, valori compresi tra 35 e 64 hanno un LH + di 1 e quindi non confermano né escludono la diagnosi di sideropenia, valori superiori a 95 hanno un LH + di 0,08 e quindi il test è molto negativo ed esclude la carenza di ferro.
Un'altra utile applicazione del LR si può vedere nell'esempio che segue. Si avverte che i dati di probabilità pre-test e LR + riportati non corrispondono a dati reali e servono solo a scopo didattico.
Una paziente di 48 anni si presenta in uno studio medico riferendo crisi di dolore toracico saltuarie, prevalentemente dopo sforzi fisici, di breve durata. Il medico che la visita pensa subito ad una angina pectoris però sa che in una popolazione non selezionata di donne di 48 anni la prevalenza di cardiopatia ischemica (quindi al probabilità pre-test) è bassa, del 2% circa. Tuttavia il medico sa anche che quella specifica paziente è ipertesa da qualche anno e soffre di diabete, inoltre le caratteristiche del dolore toracico sono abbastanza suggestive di una origine ischemica. La presenza di questi tre segni insieme (ipertensione, diabete, caratteri del dolore suggestivi) possiede un LR + per cardiopatia ischemica di 20. La probabilità pre-test del 2% diventa allora una probabilità post-test del 28%. Il medico decide di fare seguire un elettrocardiogramma da sforzo al cicloergometro e trova un sottoslivellamento del tratto ST di circa 2 mm. Questo segno possiede un LR + per cardiopatia ischemica di 22. Allora la probabilità che era del 28% prima di eseguire il test diventa una probabilità post-test del 89%. La paziente viene ricoverata e sottoposta a coronarografia che evidenzia in effetti una grave stenosi del l’arteria discendente anteriore.
L'esempio seguente invece riguarda la diagnosi di polmonite e contiene probabilità pre-test e LR + tratte dalla letteratura [3].
Si presenta in ambulatorio un paziente con malattia respiratoria acuta. In una popolazione di soggetti con tale patologia la prevalenza di polmonite (probabilità pre-test) è del 5%. Ciò significa che 5 hanno una polmonite e 95 hanno una patologia respiratoria indifferenziata. Tuttavia vi sono alcuni segni e sintomi che se presenti possono aumentare la probabilità pre-test. Per esempio la presenza di febbre ha un LR + per polmonite medio di 1.9. Questo vuol dire che la probabilità post test diventa del 9% circa. Il segno clinico tachipnea ha un LR + medio di 2,4: la probabilità pre-test che era diventata del 9%, se è presente anche tachipnea, passa al 18% circa. La tachicardia ha un LR + medio di 1,9: se è presente anche tachicardia la probabilità post-test aumenta ulteriormente e arriva al 29% circa. Infine se sono presenti anche crepitii polmonari, il cui LR + medio è di circa 2, la probabilità post-test passa dal 29% al 44%. In conclusione quasi un paziente su due con una flogosi respiratoria in cui siano associati iperpiressia, tachicardia, tachipnea e crepitti polmonari ha una polmonite. Ovviamente a questa conclusione ci si può arrivare anche su base puramente clinica basata sull'esperienza ma la quantificazione della probabilità post-test è utile in quanto permette di dire che il bicchiere può essere mezzo pieno ma anche mezzo vuoto: un po' più di un paziente su due con le caratteristiche cliniche suddette non ha una polmonite, mentre sulla base dell'esperienza si sarebbe portati a giudicarla molto più probabile.
Renato Rossi
Bibliografia
1) http://www.pillole.org/public/aspnuke/news.asp?id=3361
2) http://www.pillole.org/public/aspnuke/news.asp?id=3363
3) Grassi M. Diagnosticare il polmone malato. Occhio Clinico 2005; 7:12-14
|
 |
 |
Letto : 4034 | Torna indietro |  | |  | | 
|
 |
 |
 |
 |
|
|
|


